1T
-

1. Tall og Algebra
-

2. Røtter og Potenser
-

3. Kvadratsetninger og Annengradslikninger
-

4. Grenseverdi
-
5. Derivasjon
-

6. Andre Funksjoner
-

7. Trigonometri
Tall of Algebra
Under Utvikling
Røtter og Potenser
Under Utvikling
3. Kvadratsetninger og Annengradslikninger
Utforskningsreisen tar utgangspunkt i at elevene utvikler kvadratsetningene. Deretter følger de i de gamle grekernes fotspor for å lære seg å fullføre kvadratet, slik at de kan løse annengradslikninger ved hjelp av kvadrater. I de siste arkene kommer elevene selv frem til abc-formelen og heltallsmetoden som to andre muligheter for å løse annengradslikninger:
KVA 01 – Kvadratsetninger Elevark
KVA 02 – Kvadratsetninger i geometrisk perspektiv Elevark
KVA 03 – Faktorisering med kvadratsetninger Elevark
KVA 04 - Fullstendig kvadrat del 1 Elevark
KVA 05 - Fullstendig kvadrat del 2
KVA 06 - Binomer høyere grad
KVA 07 – Simple annengradslikninger
KVA 08 – Løs annengradslikninger med kvadrater
KVA 08A - Al-Khwarizmi's metode
KVA 09 - Fullstendig kvadrat del 3
KVA 10 - bc-Formelen
KVA 10A - abc- Formelen
KVA 11 – Heltalltmetoden
KVA 11A - Heltallmetoden for a > 1
4. Grenseverdi
levene kan bare komme til dybdeforståelse av derivasjon hvis de har gjort seg erfaringer og har blitt fortrolige med uendelige prosesser og grenseverdi. Igjen tar vi utgangspunkt hos de gamle grekere. Denne gang er i Zenons berømte paradoks om sprinteren Achilles, som ikke kunne ta igjen en treg skilpadde. Elevene oppdager også at det i noen tilfeller går an å finne summen av uendelig mange tall . Avslutningsvis undersøker elevene kvotienter der både nevner og teller nærmer seg null og kvotienten nærmer seg et tall. Dette er en ganske overraskende oppdagelse for dem og det er kjernen i derivasjon.
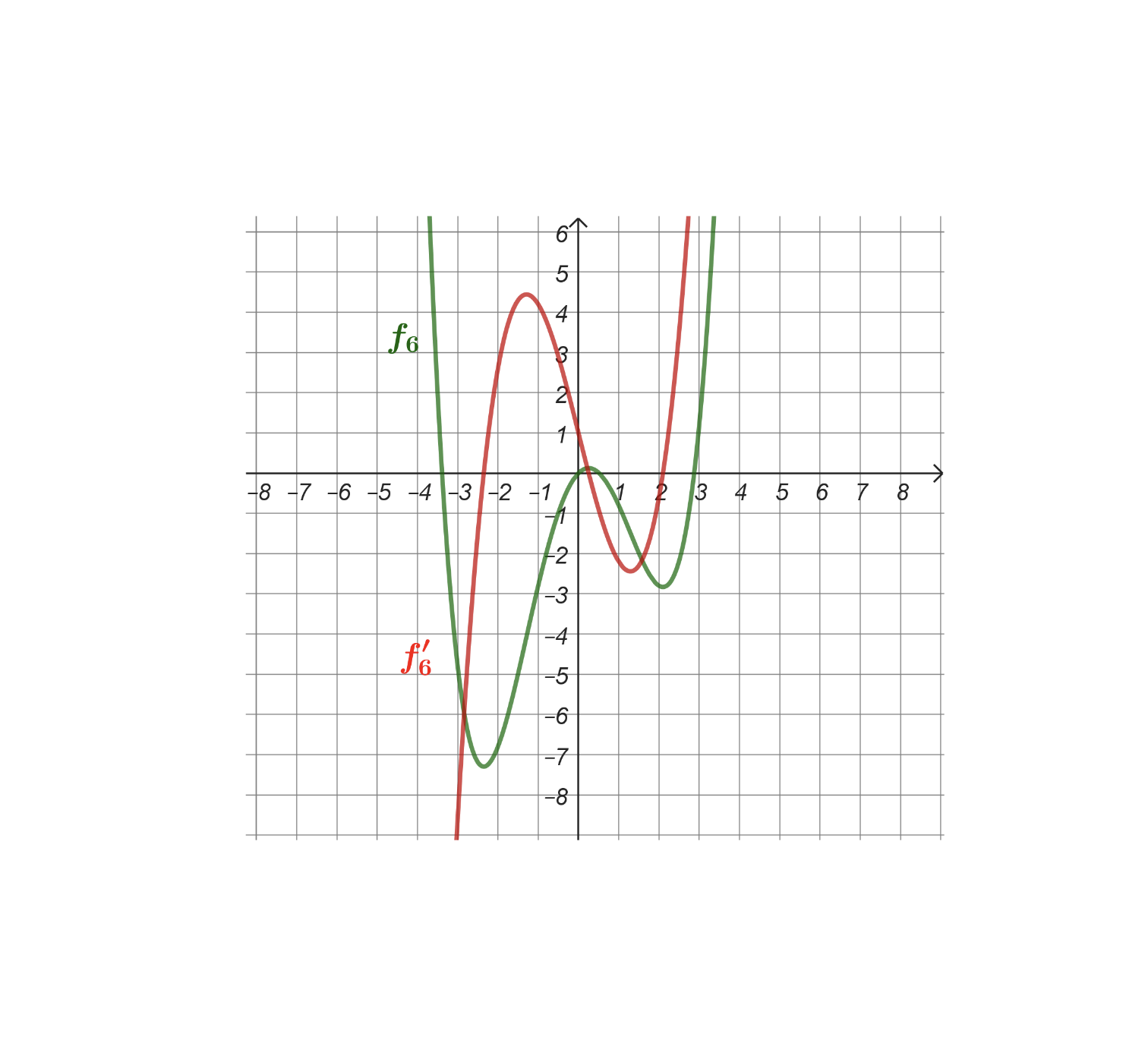
5. Derivasjon
Elevene kan bare komme til dybdeforståelse av derivasjon hvis de har gjort seg erfaringer og har blitt fortrolige med uendelige prosesser og grenseverdi. Igjen tar vi utgangspunkt hos de gamle grekere. Denne gang er i Zenons berømte paradoks om sprinteren Achilles, som ikke kunne ta igjen en treg skilpadde. Elevene oppdager også at det i noen tilfeller går an å finne summen av uendelig mange tall. De utvikler formelen . Avslutningsvis undersøker elevene kvotienter der både nevner og teller nærmer seg null og kvotienten nærmer seg et tall. Dette er en ganske overraskende oppdagelse for dem og det er kjernen i derivasjon.
Utforskningsreisen om derivasjon tar utgangspunkt i en konkret kroppslig erfaring hos elevene, nemlig et stup fra 5 meter tårnet. Mange har erfart at man har en momentanhastighet når man da rammer vannet. Men hva er denne momentanhastigheten? Og hvordan kan vi finne den? Heretter finner elevene stigningstallet for tangenten i vilkårlige punkter, først for , seinere for og for vilkårlige polynomfunksjoner. Utforskningsreisen gir også et første møte med funksjonsdrøfting og maksimeringsutfordringer.
DER 01 - Stup fra fem meter Forhåndsvisning
DER 02 Stigningstallet for en tangent del 1 Forhåndsvisning
DER 02A – To-punktformel
DER 03 - Stigningstall for tangent del 2
DER 04 – f’(xn)
DER 05 - Polynomfunksjoner Forhåndsvisning
DER 06 - Derivasjon av polynomfunksjoner
DER 07 - grafen til f' ut fra grafen for f Forhåndsvisning
DER 07A – Antideriverte
DER 08 – Funksjonsdrøfting
6. Andre Funksjoner
I Utvikling
7. Trigonometri
Utforskningsreise Trigonometri omfatter 15 ark og tar utgangspunkt i en undersøkelse av formlikhet. Til elevenes store overraskelse gjelder andre lovmessigheter for formlike trekanter enn for formlike firkanter. Dette gjør trekanter enestående når det gjeller å finne avstander man ikke kan måle. Igjen går vi i de gamle grekeres fotspor i deres utmåling av universet ved å plassere imaginære trekanter på lure måter. Sinus blir innført slik som de gamle grekere gjorde det, som forholdet mellom diameter og korde i en sirkel. Dette viser seg å ha mange fordeler. Blant annet har vi da definert sinus til alle vinkler mellom og med en gang. Dessuten gir sinussetningen nesten seg selv. Definisjonen av sinus som forholdet mellom motstående katet og hypotenus i rettvinklet trekant er et spesialtilfelle av denne klassiske definisjonen. På reisen finner elevene også ut av, at det er lurt å definere cosinus og tangens og de oppdager cosinussetningen og arealsetningen. Serien består av disse ark:
TRIG 01 - Hva er omkretsen på jorden Forhåndsvisning
TRIG 02 – Formlikhet Forhåndsvisning
TRIG 02A - Sentralprojeksjon av femkant
TRIG 02B – Rotasjon
TRIG 02C - Sentralprojeksjon av sirkel
TRIG 02D - Innskriving av kvadrat
TRIG 03 - Bruk tomlen og finn avstanden
TRIG 03A - Høyden av en flaggstang
TRIG 04 – Halvmåne Forhåndsvisning
TRIG 05 - Fullstendig solformørkelse
TRIG 05A – Måneformørkelse Forhåndsvisning
TRIG 06 - Formlike trekanter
TRIG 07 - Sinus Forhåndsvisning
TRIG 08 - Sinus setning
TRIG 09 - Sinus del 2
TRIG 10 - Thalen setning
TRIG 11 - Sinus del 3
TRIG 12- Cosinus
TRIG 13 – Tangens
TRIG 14 - Areal setning
TRIG 15 - Cosinussetning